Random Error Theory

Probability 
- The ratio of the number of times that an event should occur to the total number of possibilities
  - If event A can occur m ways and fails to occur n ways, then the probability of event A occurring is m/(m + n)
  - Probability of throwing a 1 on a fair die
    - Should occur one time
    - Will fail to occur 5 times
    - Probability is 1/(1+5) = 1/6
  - Probability of an event failing to occur is 1  − m/(m + n) 
​

- Probability is always between 0 and 1
  - 0 means there is no chance of occurrence
  - 1 means that the event will absolutely occur
​

Compound Events
- Compound event: The simultaneous occurrence of two or more events.
- The probability of a compound event is the product of each probabilities of each individual event occurring. P = P1 x P2 x … x Pn. 

Another Example​
- Assume that a tape exists that can only make a +1 ft or −1 ft when taping a distance.
- Let t be the number of ways that each error can occur
- And T be the total number of possibilities
- Then the possible occurrence of these random errors is... 

- For a distance of 1 tape length
  - Only one +1 error or one −1 can occur
- For a distance of 2 tape lengths
  - +1 and +1 occurs once with a resulting combined error (ce) of +2
  - +1 and −1 can occur twice (ce = 0)
  - −1 and −1 occurs once (ce = −2)
- For a distance of 3 tape lengths
  - +1, +1, +1 error occurs once (ce = +3)
  - −1, +1, +1; +1, −1, +1; +1, +1, −1 (ce = +1) occurs 3 times
  - −1, −1, +1; −1, +1, −1; +1, −1, −1,  (ce = −1) occurs 3 times
  - −1, −1, −1; (ce = −3) occurs 1
  - And so on…
​

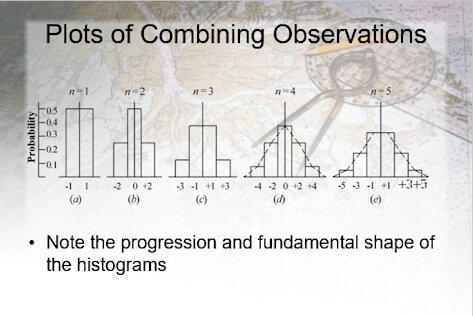
- Now
  - Draw a single line across the target tabulating the number of BBs that pierced the target along the line
  - ​Create a frequency plot of the hits versus distance from the center of the target
  - ​It may look as follows